회귀 분석(Regression Analysis): 데이터에서 패턴을 찾아 미래를 예측하는 기법

회귀 분석(Regression Analysis)은 연속형 변수 간의 관계를 분석하고, 이를 바탕으로 미래 값을 예측하는 통계적 기법입니다. 머신러닝과 데이터 과학에서 예측 모델링(Predictive Modeling)의 핵심 요소로 활용되며, 경제, 금융, 마케팅, 의료, 공학 등 다양한 분야에서 실질적인 문제 해결에 기여하고 있습니다.

이 글에서는 회귀 분석의 개념, 주요 유형, 수학적 원리, 평가 방법, Python 구현, 그리고 실전 활용 사례까지 폭넓게 다루겠습니다.

---

1. 회귀 분석이란?

1.1 회귀 분석의 기본 개념

회귀 분석은 독립 변수(X)와 종속 변수(Y) 사이의 관계를 찾고, 이를 바탕으로 새로운 X 값이 주어졌을 때 Y 값을 예측하는 기법입니다.

예제:

• 마케팅: 광고 지출(X)에 따른 매출(Y) 예측
• 경제: GDP(X)와 실업률(Y) 간의 관계 분석
• 부동산: 집 크기(X)와 가격(Y) 간의 관계 모델링

1.2 회귀 분석의 목적

✅ 변수 간의 관계 이해 (변수 영향력 분석)
✅ 미래 값 예측 (예측 모델링)
✅ 데이터 패턴 도출 및 의사결정 최적화

---

2. 회귀 분석의 주요 유형

회귀 분석에는 단순 회귀, 다중 회귀, 비선형 회귀, 로지스틱 회귀 등 다양한 유형이 존재합니다.

회귀 유형	설명	수식
단순 선형 회귀	한 개의 독립 변수를 이용한 직선 모델	Y=wX+b
다중 선형 회귀	여러 개의 독립 변수를 활용한 모델	Y=w1X1+w2X2+…+b
다항 회귀(비선형)	다항식을 이용해 곡선 형태 모델링	Y=w1X2+w2X+b
로지스틱 회귀	종속 변수가 이진 분류(0 또는 1)인 경우 사용	P(Y=1)=1/1+e−(wX+b)
릿지 & 라쏘 회귀	과적합 방지를 위한 규제 적용	L2 정규화 (릿지), L1 정규화 (라쏘)

---

3. 단순 선형 회귀 분석: 수학적 원리

3.1 선형 회귀 모델 수식

단순 선형 회귀는 한 개의 독립 변수(X)와 종속 변수(Y) 간의 관계를 나타냅니다.

Y=wX+b

여기서,

• YYY = 예측 값
• XXX = 독립 변수
• www = 기울기(Slope, 회귀 계수)
• bbb = 절편(Intercept)

예제: 광고 지출(X)과 매출(Y) 관계

\text{매출} = 10 \times \text{광고비} + 5 ]

---

3.2 비용 함수 (Loss Function)

선형 회귀 모델의 목표는 **오차(Residual, 잔차)**를 최소화하는 것입니다.

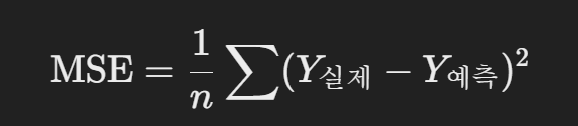
MSE(Mean Squared Error, 평균 제곱 오차)는 예측 값과 실제 값 간의 차이를 제곱하여 평균을 구하는 방식으로, 오차를 최소화하는 방향으로 모델을 학습시킵니다.

---

3.3 경사 하강법 (Gradient Descent)

회귀 계수 www와 bbb를 최적화하기 위해 **경사 하강법(Gradient Descent)**을 사용합니다.

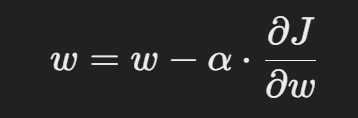
여기서,

• α= 학습률(Learning Rate)
• ∂J/∂w= 비용 함수의 기울기

경사 하강법은 반복적으로 비용을 최소화하는 방향으로 이동하며 최적의 모델을 학습합니다.

---

4. 다중 회귀 분석 (Multiple Linear Regression)

단순 선형 회귀는 하나의 독립 변수만을 사용하지만, 다중 회귀는 여러 개의 독립 변수를 활용하여 예측 모델을 만듭니다.

Y=w1X1+w2X2+…+wnXn+b

예제: 부동산 가격 예측

집 가격=50×평수+20×방 개수+10×위치 점수+5

---

5. 회귀 모델 평가 방법

모델의 성능을 평가하는 주요 지표는 다음과 같습니다.

지표	설명
MSE(Mean Squared Error)	평균 제곱 오차, 작을수록 좋음
RMSE(Root Mean Squared Error)	MSE의 제곱근, 해석이 쉬움
MAE(Mean Absolute Error)	절대값을 이용한 평균 오차
R2R^2R2 (결정 계수)	모델의 설명력 (1에 가까울수록 좋음)

---

6. Python을 활용한 회귀 분석

6.1 데이터 준비

<python>

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score

# 샘플 데이터 생성
np.random.seed(42)
X = np.random.rand(100, 1) * 10  # 0~10 사이의 랜덤 값
y = 3 * X + 5 + np.random.randn(100, 1) * 2  # 노이즈 추가

# 데이터 분할
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

---

6.2 단순 선형 회귀 모델 학습

<python>

# 모델 학습
model = LinearRegression()
model.fit(X_train, y_train)

# 예측
y_pred = model.predict(X_test)

# 모델 계수 출력
print(f"기울기(w): {model.coef_[0][0]:.2f}")
print(f"절편(b): {model.intercept_[0]:.2f}")

---

6.3 모델 평가

<python>

# 성능 평가
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)

print(f"MSE: {mse:.2f}")
print(f"R^2 Score: {r2:.2f}")

# 시각화
plt.scatter(X_test, y_test, label="Actual Data")
plt.plot(X_test, y_pred, color="red", label="Regression Line")
plt.xlabel("X")
plt.ylabel("Y")
plt.legend()
plt.show()

---

7. 회귀 분석의 활용 사례

• 마케팅: 광고 지출이 매출에 미치는 영향 분석
• 경제학: 금리와 주식 시장 간의 관계 예측
• 의료: 환자의 연령과 혈압 간의 관계 모델링
• 부동산: 아파트 가격 예측
• 기상 예측: 기온 변화에 따른 강수량 예측

---

8. 결론

✅ 회귀 분석은 데이터에서 관계를 찾고 미래를 예측하는 강력한 도구입니다.
✅ 단순 선형 회귀는 직선 관계를 분석하며, 다중 회귀는 여러 변수를 활용한 예측을 수행합니다.
✅ 현대 데이터 과학에서는 회귀 분석이 머신러닝 모델 개발의 핵심 기법으로 사용됩니다. 🚀