1. Greedy Method란?
**Greedy Method(탐욕법)**는 문제를 해결하기 위해 매 순간 최적이라고 판단되는 선택을 반복적으로 수행하여 최적의 결과를 도출하려는 알고리즘 설계 기법입니다. 각 단계에서 지역적으로 최적의 선택을 하며, 이를 통해 전역적으로 최적의 해결책을 찾고자 합니다.
1.1 핵심 개념
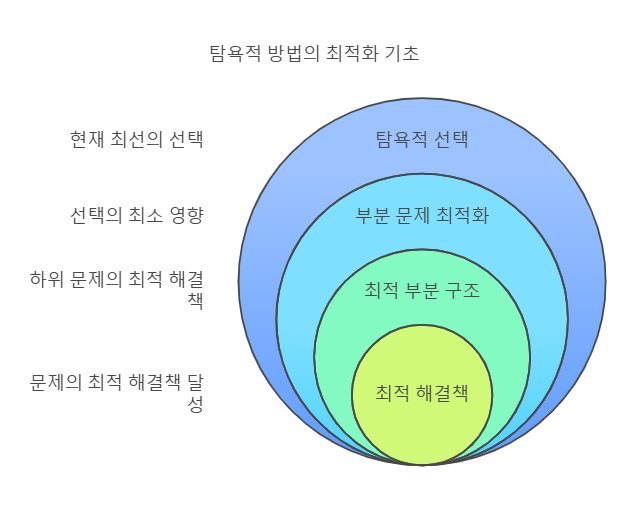
- 탐욕적 선택(Greedy Choice): 현재 상태에서 최선의 선택을 한다.
- 부분 문제 최적화: 각 선택이 이후 문제에 영향을 미치지 않거나, 영향을 최소화한다.
- 최적 부분 구조: 문제의 최적 해결책이 그 하위 문제의 최적 해결책으로 구성된다.
2. Greedy Method의 특징
2.1 장점
- 단순성과 효율성:
- 비교적 간단하게 구현 가능.
- 일반적으로 시간 복잡도가 낮음.
- 빠른 계산:
- 많은 문제에서 최적의 해를 찾을 수 있음.
2.2 단점
- 글로벌 최적 해 보장 X:
- 항상 전역 최적 해를 보장하지는 않음.
- 일부 문제에서는 그리디 선택이 최적 해를 놓칠 수 있음.
- 제약 조건 필요:
- 문제는 반드시 “최적 부분 구조”와 “탐욕적 선택 속성”을 만족해야 함.
3. Greedy Method의 조건
3.1 탐욕적 선택 속성(Greedy Choice Property)
- 정의: 현재 단계에서의 탐욕적 선택이 전역적으로도 최적의 결과로 이어질 수 있어야 함.
3.2 최적 부분 구조(Optimal Substructure)
- 정의: 문제의 최적 해결책이 그 하위 문제의 최적 해결책들로 구성될 수 있어야 함.
이 두 조건이 만족되지 않으면 Greedy Method는 최적의 해를 보장하지 못할 수 있습니다.
4. Greedy Method의 작동 방식
- 문제를 작은 단위의 단계로 분할.
- 각 단계에서 가장 최적의 선택을 수행.
- 선택한 결과를 기반으로 다음 단계로 진행.
- 모든 단계가 끝나면 결과를 조합하여 최종 해를 도출.
5. Greedy Method의 예제
5.1 최소 신장 트리(MST): Kruskal 및 Prim 알고리즘
- 문제: 그래프의 모든 정점을 연결하는 최소 비용의 간선을 찾는 문제.
- 그리디 적용: 각 단계에서 가장 낮은 가중치의 간선을 선택.
- Kruskal 알고리즘: 간선을 오름차순으로 정렬하여 순차적으로 선택.
- Prim 알고리즘: 연결된 정점 집합에서 최소 가중치 간선을 선택.
5.2 활동 선택 문제(Activity Selection Problem)
- 문제: 주어진 활동들의 시작 시간과 종료 시간에 따라 최대한 많은 활동을 선택.
- 그리디 적용: 가장 먼저 종료되는 활동을 선택하고, 이를 기준으로 겹치지 않는 활동을 반복적으로 선택.
5.3 Huffman Encoding
- 문제: 주어진 문자의 빈도에 따라 효율적인 이진 트리 기반의 인코딩 생성.
- 그리디 적용: 최소 빈도의 두 문자를 병합하여 빈도가 낮은 것부터 트리를 생성.
5.4 거스름돈 문제(Coin Change Problem)
- 문제: 최소 개수의 동전을 사용하여 특정 금액을 구성.
- 그리디 적용: 가장 큰 단위의 동전부터 차례로 선택.
- 단, 모든 경우에서 최적 해를 보장하지는 않음. (예: 1, 3, 4 단위의 동전에서는 작동하지 않음)
6. Greedy Method와 다른 알고리즘 비교
| 알고리즘 | 특징 | 적합한 문제 유형 |
|---|---|---|
| Greedy | 매 단계에서 최적의 선택 수행. | 탐욕적 선택 속성과 최적 부분 구조를 만족하는 문제. |
| Dynamic Programming (DP) | 이전 단계의 결과를 저장하여 문제 해결. | 중복되는 하위 문제를 가지며 최적 부분 구조를 만족하는 문제. |
| Brute Force | 가능한 모든 경우를 탐색. | 작은 입력 크기를 가지며 모든 가능성을 계산할 수 있는 문제. |
| Divide and Conquer | 문제를 나누어 각각 해결 후 병합. | 부분 문제들이 서로 독립적이고, 문제를 분할할 수 있는 경우. |
7. Greedy Method의 장단점 정리
7.1 장점
- 간단한 논리로 문제 해결 가능.
- 구현 및 실행 속도가 빠름.
- 그래프, 스케줄링, 네트워크 문제에서 강력한 성능.
7.2 단점
- 항상 최적의 결과를 보장하지는 않음.
- 문제의 속성을 철저히 분석해야 적합성을 판단 가능.
8. 활용 분야
8.1 네트워크
- 최소 신장 트리, 네트워크 흐름 최적화.
8.2 스케줄링
- 작업 스케줄링, 자원 할당 최적화.
8.3 데이터 압축
- Huffman 코드, 데이터 트리 구조 설계.
9. 맺음말
Greedy Method는 간단한 구현으로 효율적으로 문제를 해결할 수 있는 강력한 알고리즘 설계 방식입니다. 그러나 최적의 해를 보장하려면 문제의 속성을 철저히 분석하여 “탐욕적 선택 속성”과 “최적 부분 구조”를 만족하는지 확인해야 합니다.
적절한 상황에서 Greedy Method는 복잡한 문제를 빠르고 효과적으로 해결할 수 있는 훌륭한 도구입니다. 🚀