1. Q-러닝이란?
Q-러닝은 강화 학습(Reinforcement Learning)의 대표적인 알고리즘으로, **에이전트(Agent)**가 환경(Environment)과 상호작용하며 최적의 행동(Action)을 학습하는 기법입니다. Q-러닝은 모델 프리(Model-Free) 알고리즘으로, 환경의 **모델(전이 확률 및 보상 함수)**을 사전에 알 필요 없이 학습할 수 있습니다.
1.1 목표
Q-러닝의 목표는 **최적의 정책(Policy)**을 학습하는 것입니다.
- 정책: 주어진 상태(State)에서 최적의 행동을 결정하는 규칙.
- Q-러닝은 각 상태-행동(State-Action) 쌍에 대해 Q값(품질 값)을 계산하여 최적의 행동을 선택합니다.
2. Q-러닝의 작동 원리
Q-러닝은 Q함수를 기반으로 학습합니다. Q함수는 상태(State)와 행동(Action)의 조합에 대해 미래의 보상 기대값을 나타냅니다.
2.1 Q함수 정의
Q함수 Q(s,a)Q(s, a)Q(s,a)는 다음을 나타냅니다:
- 상태 sss에서 행동 aaa를 선택했을 때, 이후 얻을 것으로 예상되는 총 보상.
2.2 Q값 업데이트
Q-러닝은 **벨만 방정식(Bellman Equation)**을 사용하여 Q값을 반복적으로 업데이트합니다.
업데이트 공식은 다음과 같습니다:
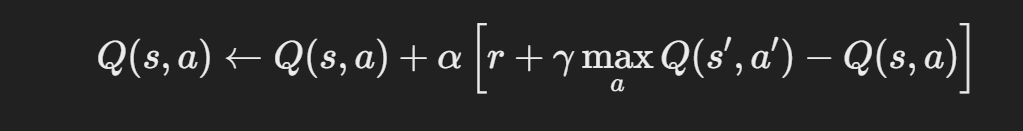
- sss: 현재 상태.
- aaa: 현재 행동.
- rrr: 행동을 수행한 후 받은 보상.
- s′s’s′: 행동을 수행한 후 도달한 다음 상태.
- α\alphaα: 학습률(Learning Rate). 새 정보의 반영 비율.
- γ\gammaγ: 할인율(Discount Factor). 미래 보상의 중요도를 나타냄.
2.3 학습 과정
- 초기화:
- 모든 Q(s,a)Q(s, a)Q(s,a) 값을 0 또는 작은 임의 값으로 초기화.
- 에피소드 실행:
- 에이전트가 초기 상태 sss에서 시작.
- 정책에 따라 행동 aaa를 선택하고 환경에서 보상 rrr을 수신.
- Q값을 업데이트.
- 상태 s′s’s′로 이동.
- 종료 상태에 도달할 때까지 반복.
- 정책 학습:
- Q(s,a)Q(s, a)Q(s,a) 값이 최적화되면 에이전트는 최적 정책을 실행.
3. Q-러닝의 주요 요소
3.1 상태(State)
- 환경의 현재 상태를 나타냅니다.
- 예: 체스 게임에서의 말 위치.
3.2 행동(Action)
- 상태에서 에이전트가 선택할 수 있는 행동.
- 예: 체스에서 특정 말을 이동.
3.3 보상(Reward)
- 행동에 따라 에이전트가 받는 즉각적인 피드백.
- 예: 체스에서 상대방 말을 잡으면 긍정적인 보상을 받음.
3.4 학습률(Learning Rate, α\alphaα)
- 새롭게 계산된 Q값을 기존 값에 얼마나 반영할지 결정.
- 값의 범위: 0≤α≤10 \leq \alpha \leq 10≤α≤1.
3.5 할인율(Discount Factor, γ\gammaγ)
- 미래 보상의 중요도를 결정.
- 값의 범위: 0≤γ≤10 \leq \gamma \leq 10≤γ≤1.
- γ=0\gamma = 0γ=0: 즉각적인 보상만 고려.
- γ\gammaγ가 클수록 미래 보상에 더 큰 가중치를 둠.
4. Q-러닝의 장점과 한계
4.1 장점
- 모델 프리 학습:
- 환경의 전이 확률과 보상 함수를 사전에 알 필요가 없음.
- 단순함:
- 알고리즘 구조가 직관적이고 구현이 간단.
- 광범위한 적용 가능성:
- 게임, 로봇 공학, 금융 등 다양한 분야에서 사용.
4.2 한계
- 대규모 상태-행동 공간:
- 상태와 행동의 조합이 많을수록 Q테이블 크기가 기하급수적으로 증가.
- 해결: 딥 Q-러닝(DQN) 사용.
- 탐험과 활용의 균형 문제:
- 탐험(Exploration): 새로운 상태를 탐색.
- 활용(Exploitation): 현재 학습된 최적 행동을 선택.
- 해결: ϵ \epsilonϵ-탐욕적 정책 사용.
- 연속형 상태/행동 공간:
- 연속적인 상태와 행동을 처리하기 어려움.
- 해결: 함수 근사(Function Approximation) 사용.
5. Q-러닝 구현 예제
5.1 간단한 Q-러닝 구현
환경: OpenAI Gym의 FrozenLake 문제
<python>
import numpy as np
import gym
# 환경 생성
env = gym.make("FrozenLake-v1", is_slippery=False)
# Q 테이블 초기화
num_states = env.observation_space.n
num_actions = env.action_space.n
Q = np.zeros((num_states, num_actions))
# 하이퍼파라미터
alpha = 0.1 # 학습률
gamma = 0.99 # 할인율
epsilon = 0.1 # 탐험률
episodes = 1000
# Q-러닝 알고리즘
for episode in range(episodes):
state = env.reset()
done = False
while not done:
# 탐험 또는 활용 선택
if np.random.rand() < epsilon:
action = env.action_space.sample() # 탐험
else:
action = np.argmax(Q[state]) # 활용
# 행동 수행 및 보상 수신
next_state, reward, done, _ = env.step(action)
# Q값 업데이트
Q[state, action] = Q[state, action] + alpha * (reward + gamma * np.max(Q[next_state]) - Q[state, action])
state = next_state
# 학습된 Q 테이블 출력
print("학습된 Q 테이블:")
print(Q)
6. Q-러닝의 응용 분야
- 게임 AI:
- 체스, 바둑, Atari 게임 등에서 최적의 전략 학습.
- 로봇 공학:
- 로봇의 경로 최적화 및 작업 학습.
- 네트워크 관리:
- 데이터 패킷 라우팅 최적화.
- 금융:
- 투자 전략 학습 및 포트폴리오 최적화.
7. Q-러닝의 확장: 딥 Q-러닝(DQN)
Q-러닝은 상태-행동 공간이 큰 경우 비효율적일 수 있습니다. 이를 해결하기 위해 **딥러닝(Deep Learning)**을 결합한 **딥 Q-러닝(DQN)**이 등장했습니다.
- Q함수 근사: Q값을 딥러닝 모델로 근사하여 대규모 상태 공간 처리.
- 경험 재플레이(Experience Replay): 과거 경험을 재사용하여 효율적인 학습.
8. 맺음말
Q-러닝은 간단하면서도 강력한 강화 학습 알고리즘으로, 환경의 모델을 사전에 알 필요 없이 학습이 가능합니다. 비록 대규모 상태-행동 공간에서 한계를 가지지만, 딥 Q-러닝과 같은 확장을 통해 더 복잡한 문제를 해결할 수 있습니다.
현실 세계의 다양한 문제에 Q-러닝을 적용하여 최적의 정책을 학습하고, AI를 활용한 의사결정 및 최적화를 실현해 보세요! 🚀
2930 Blog에서 더 알아보기
구독을 신청하면 최신 게시물을 이메일로 받아볼 수 있습니다.
