**가우시안 혼합 모델(Gaussian Mixture Model, GMM)**은 **데이터를 여러 개의 가우시안 분포(Gaussian Distribution, 정규분포)**로 표현하여 데이터 군집(Cluster)을 찾아내는 비지도 학습(unsupervised learning) 알고리즘입니다. K-평균(K-Means) 클러스터링과 유사하지만, 데이터가 단순히 원형으로 분포하지 않고 다양한 모양의 클러스터를 형성할 때도 효과적으로 사용할 수 있습니다.
이 글에서는 GMM의 개념, 원리, EM 알고리즘, GMM과 K-평균 비교, Python 구현 방법, 그리고 실전 활용 사례를 심층적으로 다룹니다.
1. 가우시안 혼합 모델(GMM)이란?
1.1 GMM의 개념
GMM은 여러 개의 가우시안 분포가 혼합된 형태로 데이터를 모델링하는 방법입니다. 각 클러스터가 하나의 가우시안 분포로 표현되며, 전체 데이터는 이러한 가우시안 분포들의 혼합으로 구성된다고 가정합니다.
- 혼합 모델(Mixture Model): 여러 확률 분포의 조합으로 구성된 확률 모델.
- 가우시안 분포(Gaussian Distribution): 평균(μ)과 분산(σ²)으로 정의되는 종 모양의 분포.
1.2 GMM의 수학적 표현
GMM은 KKK개의 가우시안 분포가 혼합된 형태로 나타낼 수 있습니다.
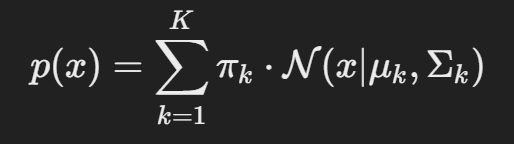
여기서,
- KKK: 혼합된 가우시안 분포의 개수(클러스터 개수).
- πk: 각 가우시안 분포의 가중치(혼합 계수), 모든 πk의 합은 1.
- N(x∣μk,Σk)): 평균 μk와 공분산 Σk을 가진 가우시안 분포.
- x: 입력 데이터.
1.3 GMM의 특징
- 확률 기반 모델: 데이터가 각 클러스터에 속할 확률을 계산.
- 다양한 형태의 클러스터: 원형뿐만 아니라 타원형, 비선형 형태의 클러스터도 탐지 가능.
- 혼합 계수 제공: 각 데이터가 특정 클러스터에 속할 확률을 제공하므로 소프트 클러스터링이 가능.
- EM 알고리즘을 사용하여 최적의 매개변수를 반복적으로 추정.
2. GMM의 작동 원리: EM 알고리즘
2.1 EM 알고리즘(Expectation-Maximization)이란?
GMM은 EM 알고리즘을 사용하여 **모델 파라미터(혼합 계수, 평균, 공분산)**를 최적화합니다.
EM 알고리즘은 **기댓값 단계(E-step)**와 **최대화 단계(M-step)**를 반복하여 확률적 모델을 최적화하는 방법입니다.
2.2 EM 알고리즘 단계
- 초기화:
- 클러스터 개수(K) 설정.
- 각 가우시안의 초기 평균(μ), 공분산(Σ), 혼합 계수(π) 무작위 설정.
- E-step (Expectation):
- 현재 추정된 파라미터로 각 데이터가 각 클러스터에 속할 확률(책임도, γ) 계산.
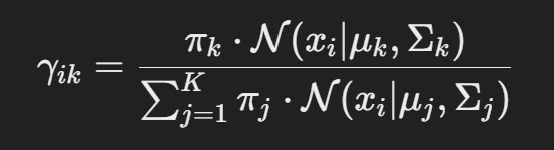
3. M-step (Maximization):
- 계산된 확률을 기반으로 각 클러스터의 새로운 평균(μ), 공분산(Σ), **혼합 계수(π)**를 업데이트.
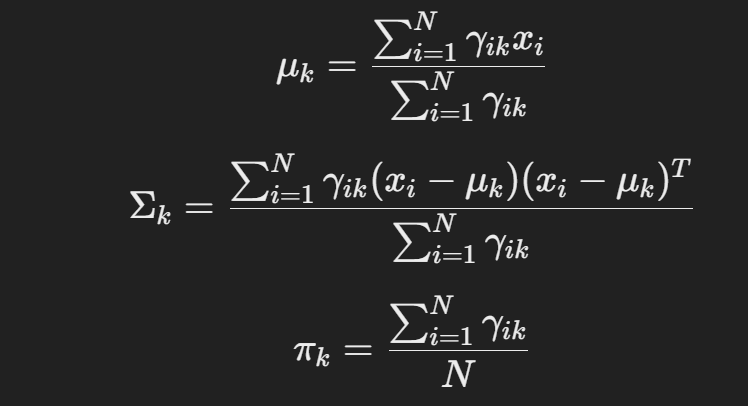
4. 수렴 조건 확인:
- 파라미터 변화가 일정 수준 이하일 때 알고리즘 종료.
- 그렇지 않으면 다시 E-step으로 반복.
3. GMM과 K-평균(K-Means) 비교
| 특징 | 가우시안 혼합 모델(GMM) | K-평균(K-Means) |
|---|---|---|
| 클러스터 형태 | 타원형, 복잡한 형태 가능 | 원형(구형)만 가능 |
| 클러스터링 방식 | 소프트 클러스터링(확률 기반) | 하드 클러스터링(이진 분류) |
| 확률 모델 | 각 데이터가 각 클러스터에 속할 확률 제공 | 각 데이터는 하나의 클러스터에만 속함 |
| 알고리즘 | EM 알고리즘 | Lloyd 알고리즘 |
| 파라미터 학습 | 평균, 공분산, 혼합 계수 | 중심점(centroid) |
| 복잡도 | 상대적으로 높은 계산량 | 상대적으로 빠름 |
| 적합한 경우 | 클러스터 모양이 비원형일 때, 소프트 클러스터링 필요할 때 | 단순한 원형 클러스터일 때 |
📌 GMM은 K-평균보다 유연하지만, 계산량이 많고 학습 시간이 오래 걸릴 수 있습니다.
4. GMM의 장단점
4.1 장점
- 비원형 데이터 클러스터링 가능: 타원형, 복잡한 형태의 클러스터에도 적용 가능.
- 확률 기반 소프트 클러스터링: 각 데이터가 여러 클러스터에 속할 확률적 추정 제공.
- 다양한 데이터 분포 처리: 데이터가 여러 개의 가우시안 분포를 따를 때 효과적.
- K-평균보다 유연: 클러스터가 꼭 원형일 필요 없음.
4.2 단점
- 복잡한 계산: EM 알고리즘으로 반복 학습하므로 계산량이 많음.
- 초기값에 민감: 초기 파라미터 설정에 따라 결과가 달라질 수 있음.
- 과적합 위험: 클러스터 개수를 과도하게 설정하면 과적합 발생 가능.
- 해석 어려움: 여러 확률 분포가 혼합되어 있으므로 해석이 직관적이지 않을 수 있음.
5. GMM의 주요 활용 사례
5.1 이미지 분할
- 이미지에서 색상, 텍스처, 모양 등 다양한 요소를 기반으로 영역(Region)을 분할.
- 예: 의료 영상에서 종양 탐지, 위성 이미지 분석.
5.2 음성 및 신호 처리
- 음성 데이터를 여러 가우시안 분포로 분해하여 음성 인식, 신호 분석.
- 예: **HMM(Hidden Markov Model)**과 결합하여 연속 음성 인식.
5.3 이상 탐지(Anomaly Detection)
- 데이터의 밀도가 낮은 영역을 이상치로 간주.
- 예: 금융 사기 탐지, 네트워크 침입 탐지.
5.4 고객 세분화
- 고객 데이터를 바탕으로 다양한 그룹으로 분류.
- 예: 마케팅 타겟팅, 개인화 추천 시스템.
6. GMM Python 구현 (Scikit-Learn)
6.1 데이터 준비
<python>
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
# 예제 데이터 생성
X, y = make_blobs(n_samples=300, centers=3, cluster_std=0.60, random_state=42)
plt.scatter(X[:, 0], X[:, 1], s=30)
plt.title("데이터 분포")
plt.show()
6.2 GMM 모델 학습
<python>
from sklearn.mixture import GaussianMixture
# 가우시안 혼합 모델 생성 (클러스터 3개)
gmm = GaussianMixture(n_components=3, random_state=42)
# 모델 학습
gmm.fit(X)
# 클러스터 예측
labels = gmm.predict(X)
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', s=30)
plt.title("GMM 클러스터링 결과")
plt.show()
6.3 혼합 계수와 파라미터 확인
<python>
print("혼합 계수 (Mixing Coefficients):", gmm.weights_)
print("평균 (Means):", gmm.means_)
print("공분산 (Covariances):", gmm.covariances_)
6.4 클러스터 확률 시각화
<python>
import numpy as np
probs = gmm.predict_proba(X)
plt.scatter(X[:, 0], X[:, 1], c=probs.max(axis=1), cmap='viridis', s=30)
plt.title("클러스터 속할 확률 (소프트 클러스터링)")
plt.colorbar()
plt.show()
7. GMM 최적화 및 활용 팁
7.1 클러스터 개수 선택
- **BIC(Bayesian Information Criterion)**과 **AIC(Akaike Information Criterion)**를 사용하여 최적의 클러스터 개수 선택.
<python>
bic = []
aic = []
for k in range(1, 10):
gmm = GaussianMixture(n_components=k, random_state=42)
gmm.fit(X)
bic.append(gmm.bic(X))
aic.append(gmm.aic(X))
plt.plot(range(1, 10), bic, label='BIC')
plt.plot(range(1, 10), aic, label='AIC')
plt.legend()
plt.show()
7.2 데이터 전처리
- **정규화(Standardization)**로 데이터의 스케일을 맞춰야 GMM이 잘 작동.
- **차원 축소(PCA)**와 함께 사용하면 계산량 감소 및 시각화 용이.
7.3 EM 알고리즘 초기값
- K-평균 초기화로 초기값 설정 시 안정적인 수렴 가능.
8. 결론
**가우시안 혼합 모델(GMM)**은 데이터를 여러 가우시안 분포로 표현하여 복잡한 클러스터링 문제를 해결하는 강력한 도구입니다. 특히 비원형 데이터와 소프트 클러스터링이 필요할 때 유용하며, 이미지 분할, 음성 인식, 이상 탐지 등 다양한 분야에서 활발히 사용됩니다.
향후 GMM은 딥러닝과 결합하여 더 복잡한 데이터 분포 학습과 실시간 클러스터링에서도 중요한 역할을 할 것으로 기대됩니다. 🚀
