[태그:] 머신러닝

로지스틱 회귀(Logistic Regression): 분류 문제를 해결하는 머신러닝 알고리즘

1. 로지스틱 회귀란?

**로지스틱 회귀(Logistic Regression)**는 **종속 변수가 이진형(또는 다중 클래스)**인 경우에 사용되는 분류 알고리즘입니다. 이름에 “회귀”가 포함되어 있지만, 실제로는 분류(Classification) 문제를 해결합니다.
로지스틱 회귀는 데이터를 분석하여 결과를 특정 클래스(또는 범주)에 속하도록 분류하는 데 사용됩니다.

2. 로지스틱 회귀의 작동 원리

로지스틱 회귀는 선형 회귀를 확장하여 0과 1 사이의 확률로 결과를 예측합니다.
다음 과정을 통해 작동합니다:

2.1 선형 함수

로지스틱 회귀는 먼저 입력 데이터 XXX와 가중치 www, 바이어스 bbb를 사용해 선형 결합을 계산합니다.

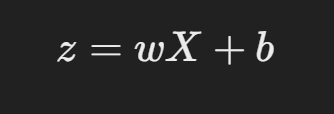
여기서:

  • XXX: 독립 변수(특성).
  • www: 가중치(모델이 학습하는 값).
  • bbb: 바이어스(편향).

2.2 시그모이드 함수(Sigmoid Function)

선형 결합 결과 zzz를 시그모이드 함수에 통과시켜 0과 1 사이의 확률 값으로 변환합니다.

​

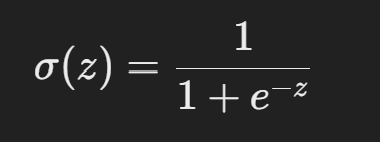
  • σ(z): 예측 확률.
  • 결과 값은 특정 클래스(예: 1)에 속할 확률로 해석됩니다.

2.3 클래스 결정

  • 확률이 특정 임계값(예: 0.5)을 초과하면 클래스 1로 예측.
  • 그렇지 않으면 클래스 0으로 예측.

3. 로지스틱 회귀의 유형

3.1 이항 로지스틱 회귀(Binary Logistic Regression)

  • 종속 변수가 두 가지 클래스(0 또는 1)로 구분되는 경우.
  • 예: 스팸 이메일(0: 스팸 아님, 1: 스팸).

3.2 다항 로지스틱 회귀(Multinomial Logistic Regression)

  • 종속 변수가 3개 이상의 클래스로 나뉘는 경우.
  • 예: 꽃의 종류(1: Iris-setosa, 2: Iris-versicolor, 3: Iris-virginica).

3.3 순서형 로지스틱 회귀(Ordinal Logistic Regression)

  • 클래스 간 순서가 있는 경우.
  • 예: 영화 평점(1: 나쁨, 2: 보통, 3: 좋음).

4. 로지스틱 회귀의 손실 함수

로지스틱 회귀는 로그 손실(Log Loss) 또는 **이항 교차 엔트로피(Binary Cross-Entropy)**를 최소화하여 모델을 학습합니다. 손실 함수는 다음과 같이 정의됩니다:

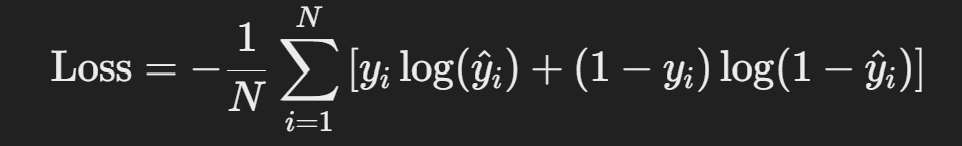
여기서:

손실 함수는 모델이 잘못된 예측을 할수록 큰 값을 가지며, 최적화를 통해 손실 값을 최소화합니다.

5. 로지스틱 회귀의 주요 하이퍼파라미터

  1. 정규화(C):
    • 과적합 방지를 위해 가중치에 패널티를 부여.
    • 값이 작을수록 더 강한 정규화를 적용.
  2. 솔버(Solver):
    • 최적화 알고리즘 선택.
    • 예: 'liblinear', 'lbfgs', 'saga'.
  3. 클래스 가중치(class_weight):
    • 클래스 불균형 문제를 해결하기 위해 클래스별 가중치 설정.

6. 로지스틱 회귀 구현 (Python)

6.1 데이터 준비

예제: 사이킷런(Sklearn)의 LogisticRegression 사용.

<python>

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score

# 데이터 로드
data = load_iris()
X, y = data.data, data.target

# 이항 분류를 위해 클래스 0과 1만 사용
X = X[y < 2]
y = y[y < 2]

# 데이터 분할
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

6.2 모델 학습

<python>

# 로지스틱 회귀 모델 생성 및 학습
model = LogisticRegression()
model.fit(X_train, y_train)

6.3 모델 평가

<python>

# 예측 및 정확도 계산
y_pred = model.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"정확도: {accuracy:.2f}")

7. 로지스틱 회귀의 장단점

7.1 장점

  1. 간단하고 해석 가능:
    • 결과가 확률 값으로 출력되어 직관적 해석 가능.
  2. 빠른 계산 속도:
    • 데이터 크기가 큰 경우에도 효율적.
  3. 정규화 옵션 제공:
    • L1, L2 정규화를 통해 과적합 방지 가능.

7.2 단점

  1. 비선형 데이터 처리 한계:
    • 입력 데이터가 선형적으로 분리되지 않으면 성능 저하.
    • 해결: 다항 특성 추가(Polynomial Features) 또는 커널 적용.
  2. 클래스 불균형 문제:
    • 한 클래스 데이터가 압도적으로 많으면 성능 저하.
    • 해결: 클래스 가중치 조정.
  3. 다수 클래스에서의 복잡성 증가:
    • 다중 클래스 분류 시 계산량 증가.

8. 로지스틱 회귀의 활용 분야

  1. 의료 진단:
    • 환자의 증상 데이터를 기반으로 질병 유무 판단.
  2. 스팸 필터링:
    • 이메일이 스팸인지 아닌지 분류.
  3. 금융:
    • 대출 승인 여부 판단.
  4. 마케팅:
    • 고객의 구매 가능성 예측.

9. 맺음말

**로지스틱 회귀(Logistic Regression)**는 간단하면서도 강력한 분류 알고리즘으로, 데이터의 관계를 모델링하고 특정 문제에 대해 예측을 수행하는 데 유용합니다. 특히 이진 분류 문제에서 자주 사용되며, 해석 가능성과 계산 효율성 덕분에 실무에서 널리 활용됩니다.

비선형 데이터나 클래스 불균형 문제에 대해 적절히 조정하면 더욱 높은 성능을 발휘할 수 있으며, 이를 통해 다양한 산업 분야에서 중요한 의사결정 도구로 활용할 수 있습니다. 🚀